Symmetric and Alternating Groups

Group:

A group $\mathit{G}$ is a set together with two operations (or more simply, functions), one called multiplication $\mathit{m}:\mathit{G}\times \mathit{G}\to \mathit{G}$ and the other called the inverse$\mathit{i}:\mathit{G}\to \mathit{G}$. These operations obey the following rules

• Associative
• Identity
• Inverse

Symmetric Group

The symmetric group on $\mathit{n}$ objects is the set of permutations rearranging $\mathit{n}$ objects. The group operation is a composition of permutations.

A permutation agrees with the notion of rearranging the set of objects. The do-nothing action is the identity permutation, i.e., $\mathit{\sigma }\left(\mathit{a}\right)=\mathit{a}$ for all $\mathit{a}\in \mathit{A}$. There are many ways to represent a permutation. One visual way is using permutation diagrams, which we will introduce via examples.

Consider the following diagrams:

Each of these diagrams represents a permutation on five objects. We’ve given the permutations the names $\mathit{\alpha },\mathit{\beta },\mathit{\sigma }$ and $\mathit{\gamma }$. The intention is to read the diagrams from the top down. It is important to remember that the numbers are referring to the position of an object, not the object itself. For example, $\mathit{\beta }$ is the permutation that sends the object in the second position to the fourth position, the object in the third position to the second position, and the object in the fourth position to the third position.

Moreover, the permutation $\mathit{\beta }$ doesn’t do anything to the objects in positions $1$ and $5$. This is called the identity permutation.

It is the standard convention to omit the composition symbol when writing down compositions in ${\mathit{S}}_{\mathit{n}}$. For example, we will simply write $\mathit{\alpha \beta }$ to denote \(\alpha\circ\beta\).

Permutation diagrams are fun to play with, but we need a more efficient way of encoding information. One way to do this is using cycle notation. Consider $\mathit{\alpha },\mathit{\beta },\mathit{\sigma }$ and $\mathit{\gamma }$ in ${\mathit{S}}_5$ from the previous examples. Below we have indicated what each permutation is equal to using cycle notation.

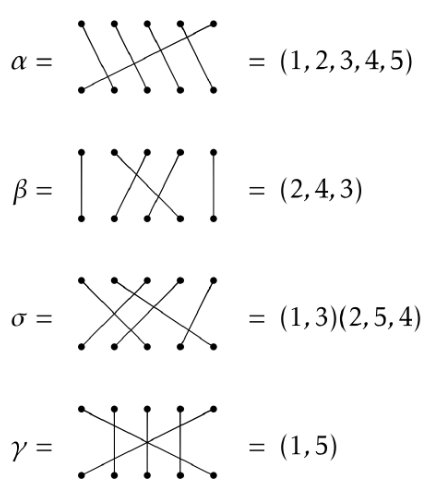
Each string of numbers enclosed by parentheses is called a cycle and if the string of numbers has length $\mathit{k}$, then we call it a $\mathit{k}$-cycle. For example, $\mathit{\alpha }$ consists of a single $5$-cycle, whereas $\mathit{\sigma }$ consists of one $2$-cycle and one $3$-cycle. In the case of $\mathit{\sigma }$ , we say that $\mathit{\sigma }$ is the product of two disjoint cycles.

If an object in position $\mathit{i}$ remains unchanged, then we don’t bother listing that number in the cycle notation. However, if we wanted to, we could use the $1$-cycle$\left(\mathit{i}\right)$ to denote this. For example, we could write $\mathit{\beta }=\left(1\right)\left(2,4,3\right)\left(5\right)$. In particular, we could denote the identity permutation in ${\mathit{S}}_5$ using $\left(1\right)\left(2\right)\left(3\right)\left(4\right)\left(5\right)$. Yet, it is common to simply use $\left(1\right)$ to denote the identity in ${\mathit{S}}_{\mathit{n}}$ for all $\mathit{n}$.